What is a system of two linear equations?

A system contains two variables; x,y and two equations

Ex. Ax+By=C

Dx+Ey=F

How do you solve a system of two linear equations?

1. Find a solution to fit the pair of variables and make the equation true.

Solution: an ordered pair of x,y

Ex. 3x-2y=2

x+2y=6

If you are given an order pair, plug both in to check which one fits.

a.) (2,2)

b.) (0,-1)

3(2)-2(2)=2

6-4=2

2+2(2)=6

2+4=6

→ Both check so A pair is a solution, now try B pair.

3(0)-2(-1)=2

0+2=2

0+2(-1)=6

0-2=-2

→ B is not a solution because the second equation does not check.

What if NO solution pair is given?

Solving equations using graphs

If no solution pair is given, then you can try solving graphically.

You are given the following system with no order pair, you must graph it in order to find its solution pair.

3x-y=7

2x+3y=1

There are many methods to graph the system; y=mx+b or you can create an x,y table to plot the points.

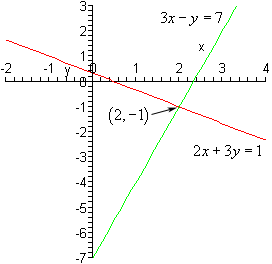
Once you graph the equation, you find that the solution pair is (2,-1)

It is encouraged to plug in the pair to make sure the system checks.

3(2)-(-1)=7

6+1=7

2(2)+3(-1)=1

4-3=1

→The solution pair checks when inserted into the linear system equation thus, you know that (2,-1) is the correct answer.

Linear Systems with One, Infinite, or No Solutions

When graphed, a system can have more than one solution, infinite or no solutions at all.

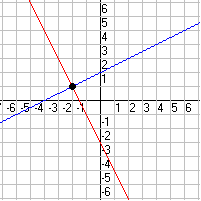
One Solution : When two lines intercept, the interception point is the solution.

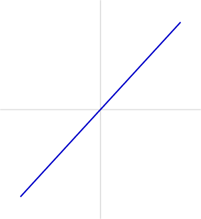
Infinite Solutions: The graph contains only one single line.

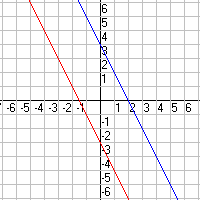
No Solution: The graph contains parallel lines and no interception point.

Think you're ready?

Now you try solving some problems to see how well you do!

Checking solution of a linear system

*Plug in solutions to find which pair is the solution of the system.

1.a) (3,2) 6x+2y=20

b) (-2,5) 3x+4y=17

2.a) (-4,-2) 5x-y=16

b) (3,-1) x+y=2

Solving a system by the graphing method

* Graph the linear system equation and find the solution.

3.3x+4y=-10

-7x-y=-10

4. y=5x

y=x+4

Systems with Many or No Solutions

*Find how many solutions the following graphs have.

5. 6.